工程问题是历年公务员考试的重点题型，几乎每次考试都会涉及。对于工程问题，我们一般的作答方法有赋值法和列方程法两种。可是面对具体问题时该如何赋值求解却令很多考生困惑不已。下面通过一道例题来谈一下赋值的方法。

　　【例】

　　某工厂的一个生产小组，当每个工人都在岗位工作，9小时可以完成一项生产任务。如果交换工人甲和乙的岗位，其他人不变，可提前1小时完成任务；如果交换工人丙和丁的岗位，其他人不变，也可以提前1小时完成任务。如果同时交换甲和乙，丙和丁的岗位，其他人不变，可以提前多少时间完成（  ）

　　A．1.4小时         B．1.8小时        C．2小时         D．2.4小时

　　【错误解析】

　　选C。根据题意，甲、乙交换岗位可以提前1小时完成任务，丙、丁交换岗位也可以提前1小时完成任务，那么同时交换甲和乙，丙和丁的岗位可以提前1+1=2（小时）完成任务，因此C项当选。

　　【错解门诊】

　　上述解析错在没有意识到只交换甲、乙或者丙、丁的时候，没交换的丙、丁或者甲、乙仍在按原来的工作效率工作，所以同时交换甲和乙，丙和丁所节约的时间必然不等于2小时，C项错误。

　　【正确解析】

　　选B。解法一：根据题意，将工作总量设为1，则原来的整体工作效率为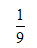。交换工人甲和乙的岗位或者交换工人丙和丁的岗位都使整体工作效率变成了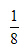，即整体工作效率都提高了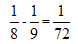，那么同时交换工人甲和乙、丙和丁的岗位后，整体工作效率变为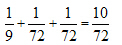，工作时间变为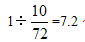小时，比原来提前9-7.2=1.8（小时）。

　　解法二：根据题意，将工作总量设为72，则原来的整体工作效率为8。已知交换工人甲和乙的岗位后可提前1小时完成任务，那么交换后的整体工作效率为9，比原来提高了9-8＝1。同理可知，交换工人丙和丁的岗位后，整体工作效率也提高了1。所以，同时交换工人甲和乙、丙和丁的岗位后，整体工作效率变为8＋1＋1＝10，工作时间变为72÷10＝7.2（小时），也就是说可以提前9－7.2=1.8（小时）完成生产任务，因此B项正确。

　　【指点迷津】

　　综合上述两种解法可以看出，将工作总量设为“72”比设为“1”要来得简便，所以说赋值的不同直接决定了运算量的大小。

　　赋值要因题而异，一般根据作答的简便性将工作总量设为某个便于计算的数字，比如上述例题我们就把工作总量设成了时间的公倍数，这样就可以避免分数运算，提高解题速度。

　　利用赋值法求解工程问题需要注意两点，一是要牢记工程问题的核心公式“工程总量=工作效率×工作时间”，二是要熟练掌握两类题型的赋值方法：（1）对于题干中告知工作时间的工程问题，我们需要将工作总量赋值为时间的公倍数；（2）对于题干中告知工作效率之比的工程问题，我们需要对工作效率赋值。

　　>>>点击可进入争议易错题专栏